www.ekivolos.gr          

   http://ekivolosblog.wordpress.com

    ΕΠΙΚΟΙΝΩΝΙΑ: ekivolos@gmail.com

                                  ekivolos_@hotmail.com

                                  ekivolos@ekivolos.gr

«Όποιος σκέπτεται σήμερα, σκέπτεται ελληνικά,

έστω κι αν δεν το υποπτεύεται.»

                                                                                                                 Jacqueline de Romilly

«Κάθε λαός είναι υπερήφανος για την πνευματική του κτήση. Αλλά η ελληνική φυλή στέκεται ψηλότερα από κάθε άλλη, διότι έχει τούτο το προσόν, να είναι η μητέρα παντός πολιτισμού.» 

                                                                                                                                                                     U.Wilamowitz

ΕΣΤΙΑΖΟΥΜΕ ΣΤΟΝ ΑΡΧΑΙΟ ΕΛΛΗΝΙΚΟ ΠΟΛΙΤΙΣΜΟ

«Τό ἑλληνικό μέτρον εἶναι τό πένθος τοῦ Λόγου»

Παναγιώτης Στάμος

Κλασσικά κείμενα-αναλύσεις

Εργαλεία

Φιλολόγων

Συνδέσεις

Εμείς και οι Αρχαίοι

Η Αθηναϊκή δημοκρατία

Αρχαία

Σπάρτη

ΣΧΕΤΙΚΗ

ΑΡΘΡΟΓΡΑΦΙΑ

Θουκυδίδης

Το Αθηναϊκό πολίτευμα 

 

Το άπειρο και τα παράδοξα του Ζήνωνα

 

Καραγιάννη Άννα

 

Η έννοια του απείρου είναι τόσο αρχαία όσο και η Ιόνιος Φιλοσοφία με το οποίο ασχολήθηκε πρώτη. Το “άπειρο”ανέκαθεν προξενούσε και προξενεί αρκετές δυσκολίες και προβλήματα στον καθορισμό του όπως και στην κατανόησή του. Με την έννοια “άπειρο” εννοούμε συνήθως κάτι το οποίο αντίκειται στο πεπερασμένο, κάτι χωρίς πέρας, κάτι έξω από το οποίο δεν υπάρχει τίποτα, κάτι το οποίο δεν επιδέχεται περαιτέρω αύξηση. Το άπειρο προκάλεσε από την αρχή διαφορές, αντινομίες, πολλές από τις οποίες αποτελούν μέχρι σήμερα αντικείμενο μελέτης. Θα αρκεστούμε στα 4 γνωστά σοφίσματα του Ζήνωνα του Ελεάτη (496-429 π.Χ.). Αυτά σήμερα έχουν ιστορική μόνο σημασία.

  

 

Το Παράδοξο της Διχοτομίας

 

 Το συγκεκριμένο Παράδοξο καταλήγει στο συμπέρασμα ότι “ η κίνηση είναι αδύνατη “διότι ο, τι κινείται, πριν φτάσει στο τέρμα του πρέπει να φτάσει στη μέση της πορείας του.

Ο Ζήνωνας λέει ότι για να μεταβεί ένα σώμα από μια θέση Α σε μια θέση Β οφείλει να διανύσει το μισό της απόστασης ΑΒ. Στη συνέχεια το μισό του υπολοίπου, ακολούθως το μισό του νέου υπολοίπου και ούτω καθ’ εξής.Οι αποστάσεις αυτές γίνονται συνεχώς μικρότερες, αλλά απαιτείται για κάθε μια απ’ αυτές ένας ορισμένος χρόνος για να διανυθεί. Και έτσι συμπέρανε ότι “το άθροισμα ενός απείρου αριθμού ορισμένων χρονικών διαστημάτων οφείλει να είναι άπειρο”.Κατά συνέπεια η πραγματικότητα της κίνησης και ακριβέστερα της έκτασης είναι αδύνατη.

Γι’ αυτή την αντινομία έχουν προταθεί αρκετές λύσεις. Μια από αυτές θεωρεί ότι το λάθος του συλλογισμού έγκειται στην αληθοφανή πρόταση “το άθροισμα ενός απείρου αριθμού ορισμένων χρονικών διαστημάτων είναι άπειρο”. Αυτή η πρόταση ισχύει αλλά όχι πάντα.

Ας υποθέσουμε για παράδειγμα ότι (ΑΒ) = 2 Κm και η ταχύτητα του κινητού είναι u = 1 Km/min. Τότε το μισό της απόστασης έστω (ΑΜ₁) θα διανυθεί σε χρόνο t₁ = 1 min ,το μισό του υπολοίπου απόστασης το (Μ₁Μ₂) σε χρόνο t₂ = 1/2 ,το μισό του υπολοίπου, δηλ. το (Μ₂Μ₃) σε χρόνο t₃ = 1/4 min, κ.τ.λ. Έτσι ο χρόνος t που απαιτείται για να διανυθεί η απόσταση (ΑΒ) δίνεται από τη σειρά t=t₁+t₂+.....+t_n+... _{, δηλαδή t = 1+1/2 +1/4 +...+1/2ν+...}

_{Το άθροισμα, όμως , δεν είναι άπειρο. Ισχύει ότι t® 2,αλλά ποτέ δεν το υπερβαίνει. Κατά συνέπεια ο χρόνος είναι t = 2 min και όχι άπειρος. Έτσι, απο+ρρίπτεται το συμπέρασμα του Ζήνωνα ότι η κίνηση είναι αδύνατη.}

  

 

Το Παράδοξο του Αχιλλέα και της Χελώνας.

 

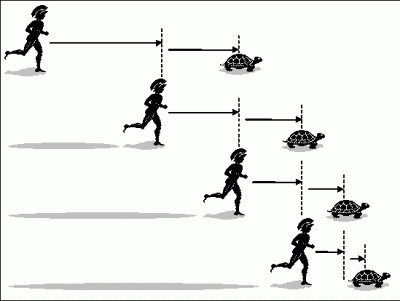
 Το συγκεκριμένο παράδειγμα καταλήγει στο συμπέρασμα ότι “ο βραδύτερος ουδέποτε θα προσπεραστεί από τον ταχύτερο’’.

Για να παρουσιαστεί αυτή η αντινομία πιο κατανοητή ας υποθέσουμε ότι η χελώνα προσπερνά τον Αχιλλέα 100 m και ότι η ταχύτητα u_A του Αχιλλέα είναι u_A=10 m/sec και της χελώνας, u_x, είναι u_x=1 m/sec. Τότε ο Αχιλλέας σε χρόνο t₁=10 sec θα διανύσει την απόσταση (ΑΧ₁)=100 m, την οποία τον προσπερνούσε η χελώνα. Κατά τη διάρκεια αυτού του χρόνου t₁ η χελώνα θα διανύσει το διάστημα (x_1x2) =10 m. Στη συνέχεια για να διατρέξει αυτή την απόσταση ο Αχιλλέας θα χρειαστεί χρόνο t₂ =1 sec. Κατά το χρόνο t₂ η χελώνα θα διανύσει το διάστημα (x_2x3) =1 m και ο Αχιλλέας θα το διατρέξει σε χρόνο t₃ =1/10 sec.Η κίνηση αυτή θα συνεχίζεται επ’ άπειρο. Έτσι κατέληξε ο Ζήνων, ότι ο Αχιλλέας δε θα φτάσει ποτέ τη χελώνα.

Όμως και η αντινομία αυτή αίρεται όπως και η προηγούμενη. Έτσι ο χρόνος t θα δίνεται από τη σχέσηt=t₁+t₂+.....+t_{n  ή t=10+1+1/10+...+1/10}ν_{. Όμως και αυτή η σειρά έχει πεπερασμένο άθροισμα και είναι ίσο με t=11}1/9 sec.

 

  

Το Παράδοξο του “πετώντος βέλους”.

 

 Το παράδοξο αυτό καταλήγει στο συμπέρασμα ότι ”αν κάτι είναι σε ηρεμία ή κίνηση σε χώρο ίσο με τον εαυτό του και αν ο,τι κινείται θεωρείται πάντοτε στιγμιαίως, τότε το βέλος στο πέταγμά του είναι ακίνητο ”.

Ας δεχτούμε ότι ένα βέλος τίθεται σε κίνηση ανάμεσα σε δύο σημεία Σ₁ και Σ₂ και μεταξύ των χρόνων t₁ και t₂.Ανάμεσα σ’ αυτά υπάρχουν πολλά σημεία Σn και αντίστοιχα κατά την κίνηση πολλά χρονικά σημεία t_n με n=1,2,3,...

Το σύνολο των χωρικών σημείων που καταλαμβάνει το βέλος είναι ο χώρος που ισούται προς τις διαστάσεις αυτού του αντικειμένου. Αν λοιπόν φανταστούμε κατά συστοιχία σύνολα αντιληπτικών χωρικών σημείων, απ’ αυτά που το σύνολό τους ισούται προς το διάστημα το οποίο διανύει το κινούμενο αντικείμενο και ανάλογα αν φανταστούμε κατά συστοιχία σύνολα αντιληπτικών χρονικών σημείων της διάρκειας της κίνησής του , τότε τα σημεία του αντικειμένου παρουσιάζονται ακίνητα μέσα στα χωροχρονικά αυτά σημεία. Έτσι όλη η κίνηση του αντικειμένου, η οποία προϋποτίθεται στην εμπειρία μας ως συνεχής, δεν είναι παρά μια εικόνα που συντίθεται από ασυνεχείς φάσεις, δηλαδή μια “κινηματογραφική” και όχι φυσική κίνηση.

 

  

Το Παράδοξο του Σταδίου.

 

 Ας φανταστούμε τρείς παράλληλες σειρές σημείων Α,Β,Γ από τις οποίες η σειρά Α μένει ακίνητη και οι άλλες δύο κινούνται με ίση ταχύτητα προς αντίθετες κατευθύνσεις μπροστά από τη σειρά Α. Τα σημεία Β κινούνται προς τα δεξιά ενώ συγχρόνως τα σημεία Γ κινούνται προς την αντίθετη κατεύθυνση με την ίδια ταχύτητα και ρυθμό με το Β.

Έτσι, κάποια ορισμένη στιγμή το Β¹, το Α³ και το Γ¹ βρίσκονται όλα στο ίδιο ύψος. Στη συνέχεια το Β¹ θα είναι απέναντι από το Α⁴, το Γ¹ απέναντι από το Α² και το Β³ απέναντι από το Α². Δηλαδή το Γ¹ είχε ευθυγραμμιστεί με το Β² πριν ευθυγραμμιστεί με το Β³. Αυτό, όμως ,σημαίνει ότι η κίνηση θα μπορούσε να θεωρηθεί ότι συντελείται συνεχώς δια μέσου των διαδοχικά διαιρετών μερών της χωροχρονικής έκτασης.

Η αντινομική μορφή των επιχειρημάτων αυτών οργανώνεται γύρω από τη θέση ότι η πορεία διαίρεσης και σύνθεσης της χωρικής και χρονικής έκτασης οδηγεί στο άπειρο.

Η πραγματικότητα του απείρου υπήρξε η πηγή πολλών διαφωνιών και αντιθέσεων μεταξύ των φιλοσόφων και μεταξύ των μαθηματικών σε όλους τους αιώνες. Γι’ αυτό αρκετοί φιλόσοφοι και μαθηματικοί κατά καιρούς αναγκάστηκαν να το αρνηθούν για να αποφύγουν τις δυσκολίες και τα παράδοξά του. Έτσι, ο Αμερικανός E.Northrop πιστεύει ότι “το άπειρο είναι ένας από τους καθαρούς εχθρούς της ησυχίας του πνεύματος των μαθηματικών”. Πράγματι, το άπειρο απασχολεί συνεχώς από την ανακάλυψή του το ανθρώπινο πνεύμα και είναι η αιτία αρκετών από τα μαθηματικά σοφίσματα, παράδοξα, και αντινομίες, δεν είναι όμως, μαθηματικά παράλογα.

 Βιβλιογραφία:

 

 Το παραπάνω κείμενο είναι απόσπασμα της διάλεξης του κ. Γ.Κ.Μαυρικάκη: ”Οι σύγχρονες απόψεις περί του απείρου” στην Ε.Μ.Ε. έτους 1964 καθώς και του περιοδικού Δευκαλίων, τεύχος 11ο, “Προσωκρατική φιλοσοφία”.

 

 

 

Τα παράδοξα του Ζήνωνα-2

 

Πιστεύετε ότι υπάρχουν άπειρα πράγματα; Τότε ο χώρος δεν υπάρχει. Πιστεύετε ότι η κίνηση είναι απείρως διχοτομήσιμη; Τότε η κίνηση είναι αδύνατη! Σε αυτά τα λογικά συμπεράσματα κατέληξε ο Ζήνωνας, διατυπωμένα μέσα από τα γνωστά του παράδοξα.

Ωστόσο, πριν διατυπώσουμε αυτά τα παράδοξα, θα ήταν χρήσιμο να κατανοήσουμε το εννοιολογικό πλαίσιο σύμφωνα με το οποίο ο Ζήνωνας κινήθηκε. Πρώτον, ο Ζήνωνας είχε ως σκοπό να υπερασπιστεί τον Παρμενίδη, ο οποίος πίστευε στη ‘μία και μοναδική αλήθεια και πραγματικότητα.’ Ο ίδιος είχε πει ότι ‘Εν τω Παν.’ Αυτό σημαίνει, σύμφωνα πάντα με την άποψη του Παρμενίδη, ότι η αλλαγή είναι αδύνατη. Με άλλα λόγια, κάθε έννοια της κίνησης ή της πολυπλοκότητας των φυσικών φαινομένων θα είναι ψευδαίσθηση, αφού θα υπάρχει μία αλήθεια. Μέσα σε αυτό το κοσμοϊστορικό πλαίσιο, μπορούμε να συνεχίσουμε καταγράφοντας τα παράδοξα του Ζήνωνα:

 

 

Το παράδοξο του ‘απείρου’

 

- Αν υπάρχουν πολλά, τότε θα είναι άπειρα. Γιατί πάντα θα υπάρχουν κι άλλα ανάμεσα στα προηγούμενα, κοκ.

- Αν υπάρχουν άπειρα πράγματα θα είναι απείρως μικρά. Αν όμως αυτά τα απειροστά προστεθούν, το τελικό αποτέλεσμα θα είναι τίποτα.

- Αν καθένα από αυτά κατέχει και μια θέση, τότε θα υπάρχει πάντα μια νέα θέση ανάμεσα στις προηγούμενες, κοκ.

Άρα το άπειρο δεν μπορεί να υπάρχει.

 

 

 ‘Το παράδοξο της κίνησης’

 

- Για να διανυθεί μια απόσταση, πρώτα πρέπει να διανυθεί η μισή, και πριν η μισή της μισής, κοκ.

- Αν ένας δρομέας θέλει να φτάσει έναν άλλον που προπορεύεται, θα πρέπει να διανύσει έναν άπειρο αριθμό ενδιάμεσων σταδίων. Άρα δεν θα τον φτάσει ποτέ.

- Αν ένα βέλος που πετάει, κάθε χρονική στιγμή είναι ακίνητο, τότε είναι ακίνητο συνέχεια.

Έτσι η κίνηση είναι αδύνατη.

Θα ήθελα εδώ να πω το εξής. Τα ‘παράδοξα του Ζήνωνα’ μας έχουν δοθεί από τρίτους, από τον Αριστοτέλη για παράδειγμα, και ύστερα από επάλληλες εκδοχές και μεταφράσεις. Έχουν διατυπωθεί με διάφορους τρόπους και ονομασίες, με τις όποιες παρερμηνείες. Όποια κι αν είναι η συλλογιστική, τα παράδοξα αυτά είναι παράδοξα λογικής και ως εκ τούτου κάποιος μπορεί να πει ότι ισχύουν ή ότι δεν ισχύουν, ανάλογα με τα αξιώματα και τους κανόνες επαγωγής που θα χρησιμοποιήσει. Επίσης, είναι πολύ δύσκολο να κατανοήσουμε το αρχικό πνεύμα των παραδόξων και τους σκοπούς που αυτά επιχειρούν να πετύχουν, εξαιτίας της μεγάλης χρονικής απόστασης από την εποχή που πρωτοδιατυπώθηκαν, καθώς και από τις, αγεφύρωτες ως έναν βαθμό, εννοιολογικές αποκλίσεις από τις αντίστοιχες σημερινές έννοιες.

Με μία φράση, η μέθοδος που χρησιμοποιεί ο Ζήνωνας είναι αυτό που θα ονομάσω ‘λογική διχοτόμηση.’ Το αρχικό επιχείρημα χωρίζεται σε ολοένα και επιμέρους επιχειρήματα, τα οποία στη συνέχεια μπορούν να ανασυντεθούν έτσι ώστε να υπάρξει ένα, στα πλαίσια της λογικής επαγωγής πάντα, έγκυρο συμπέρασμα.

Θα ήθελα να αναφέρω εδώ ένα συνηθισμένο παράδειγμα που χρησιμοποιείται για την άρση των παραδόξων του Ζήνωνα. Πρόκειται για τις λεγόμενες συγκλίνουσες σειρές, γνωστές ήδη από τον Αρχιμήδη. Αν θεωρήσουμε, λόγου χάρη, το παράδοξο του δρομέα (γνωστό και ως ‘ο Αχιλλέας και η χελώνα’), θα δούμε ότι χωρίζοντας μιαν απόσταση στο μισό ξανά και ξανά, παίρνουμε μια απλή γεωμετρική πρόοδο της μορφής 1/2+1/4+1/8+1/16+... η οποία, αθροίζοντας τους όρους, συγκλίνει και δίνει άθροισμα 1. Με αυτήν την έννοια, ο ‘Αχιλλέας’ θα διανύσει ακριβώς την απαιτούμενη απόσταση και θα φτάσει τη χελώνα. Ωστόσο, και πάλι, δεν καταρρίψαμε το επιχείρημα του Ζήνωνα: Η ίδια η γεωμετρική πρόοδος είναι άπειρη, αποτελείται δηλαδή από άπειρους όρους και για να πάρουμε την μονάδα ως τελικό αποτέλεσμα θα πρέπει να κάνουμε ένα άπειρο αριθμό πράξεων (αυτό ακριβώς θα μας έλεγε ο Ζήνωνας!)

Ένας άλλος τρόπος να επιλύσουμε τα παράδοξα του Ζήνωνα είναι μέσω της σύγχρονης κβαντικής φυσικής. Σύμφωνα με αυτήν, ο χώρος (απόσταση) είναι κβαντωμένος. Η κβαντική φυσική μας δίνει το ελάχιστο δυνατό μήκος που μπορούμε να ‘κόψουμε’ ένα ευθύγραμμο τμήμα, όπου αυτό το ελάχιστο μήκος ονομάζεται μήκος Plank. Πρόκειται για μια πολύ μικρή μονάδα μήκους (ισούται περίπου με 1.616×10^−35 μέτρα) αλλά είναι θεμελιώδης και πεπερασμένη. Με άλλα λόγια, αν στο προηγούμενο παράδειγμα ο Αχιλλέας απέχει 100 μέτρα από τη χελώνα, η απόσταση που έχει να διανύσει δεν είναι άπειρη αλλά αποτελείται από 100/(1.616×10^-35 )= 61.87×10^35 ενδιάμεσα ‘θεμελιώδη’ βήματα. Έτσι το παράδοξο του Ζήνωνα άρεται. Αν βέβαια σκεφτούμε ότι μπορούμε να διαιρέσουμε το μήκος Plank σε ακόμα μικρότερα μήκη, το παράδοξο επανέρχεται και πάλι…

Ο Ζήνωνας, με τα παράδοξά του, στην πραγματικότητα έθεσε τα θεμέλια αυτού που σήμερα ονομάζεται θεωρία συνόλων (Set Theory), καθώς επίσης και τα όρια ισχύος της μηχανικής (κινηματικής ειδικά) και του απειροστικού λογισμού. Ακριβώς αυτά τα παράδοξα που διατύπωσε ο Ζήνωνας είναι και τα παράδοξα της σύγχρονης επιστήμης σχετικά με τις έννοιες του χώρου του χρόνου και του απείρου. Σε ότι αφορά τα λεγόμενα απειροσύνολα, ο Cantor ήταν ο πρώτος που θεώρησε ότι δεν έχουν όλα τα απειροσύνολα το ίδιο μέγεθος, ούτε και ότι είναι απαραίτητα μη μετρήσιμα. Επίσης, στη σύγχρονη μηχανική η κίνηση γίνεται αντιληπτή και μετρήσιμη μέσα από την έννοια της ταχύτητας. Η μεταβολή της θέσης ενός σώματος σε κάποια χρονική στιγμή (στιγμιαία ταχύτητα) ορίζεται μέσω των απειροστών dx/dt. Αμέσως, όμως ο Ζήνωνας επανέρχεται δριμύτερος και μας ρωτά: Πώς είναι δυνατό αν η μετατόπιση dx είναι απειροστή (δηλαδή τείνει στο μηδέν) ένα σώμα να διανύσει μια απόσταση μη μηδενική;

Ακόμη κι αν απορρίψουμε την πεποίθηση του Ζήνωνα ότι η κίνηση είναι μια ψευδαίσθηση, και ότι η αλήθεια είναι μία και αναλλοίωτη, οφείλουμε, τελικά, να ομολογήσουμε ότι, κατόπιν όλων αυτών, κάτι θα πρέπει να έχει αλλάξει στον τρόπο που αντιλαμβανόμαστε την έννοια του απείρου, το χρόνο, το χώρο και την κίνηση μέσα σ’ αυτόν. Στην πραγματικότητα, αυτό που αποκαλούμε ‘ταχύτητα’ δεν είναι μια συνεχής κίνηση ‘μέσα από όλα τα ενδιάμεσα σημεία του χώρου,’ αλλά ένα είδος ‘αποτελέσματος’ από ‘το αρχικό σημείο στο τελικό σημείο,’ όπου ανάμεσα σε αυτά τα σημεία υπάρχει το ‘κενό.’ Ίσως, δηλαδή, ο χώρος και χρόνος να έχουν να κάνουν περισσότερο με μια συνέπεια του τρόπου που ο άνθρωπος αντιλαμβάνεται τη μεταβολή, (ή την ακινησία) παρά με κάποια αντικειμενική φυσική πραγματικότητα, ενώ η έννοια του απείρου να έχει να κάνει με την ίδια τη διαδικασία της ανθρώπινης λογικής.

 

 

Πηγή: http://christselentis.blogspot.gr/2009/07/blog-post_03.html