Η Κοσμολογία του Πλάτωνα μέσα από τον
Τίμαιο
ΔΟΡΤΣΙΟΣ ΚΩΝΣΤΑΝΤΙΝΟΣ,
ΑΜΑΡΑΝΤΙΔΗΣ ΣΑΒΒΑΣ
Περίληψη
Ο Πλάτων, ο μεγάλος φιλόσοφος του 4ου π.Χ. αιώνα,
είναι εκείνος που πίστευε στην ύπαρξη του κόσμου των ιδεών και θεωρούσε τον
άνθρωπο δέσμιο του αισθητού κόσμου. Στον Τίμαιο αναλύει τις απόψεις του για τη
δημιουργία του κόσμου και εισάγει με τη βοήθεια των μαθηματικών ένα μοντέλο
στηριζόμενο στα τέσσερα κανονικά στερεά. Το τετράεδρο, το οκτάεδρο, το
εικοσάεδρο, και τον κύβο. Ως βασικές δομικές μονάδες θεωρεί τα δύο ορθογώνια
τρίγωνα. Το ορθογώνιο ισοσκελές και το ορθογώνιο σκαληνό το οποίο προκύπτει από
το ισόπλευρο τρίγωνο αν το χωρίσουμε σε δύο ή έξι ίσα μέρη με το ένα ή τα τρία
ύψη του. Το ιδεαλιστικό αυτό μοντέλο διαφέρει από το υλιστικό μοντέλο του
Δημόκριτου γιατί ο Πλάτων θεωρεί, ως βασική προΰπόθεση για την ανακάλυψη του
κόσμου των ιδεών, τη μελέτη και χρήση των Μαθηματικών. Σήμερα οι απόψεις του
Πλάτωνα έρχονται στην επικαιρότητα με την εστίαση των αστροφυσικών στις
ιδιότητες του κανονικού δωδεκαέδρου, με το οποίο ο φιλόσοφος συμβόλιζε το
Σύμπαν.
-
Εισαγωγικά
«Ο ελληνικός πολιτισμός τον 4ο αιώνα π.Χ. παρουσιάζει τεράστιο
ενδιαφέρον, γιατί βλέπουμε πώς μια χώρα, που συνερχόταν από τον κλονισμό του
Πελοποννησιακού Πολέμου, μπόρεσε να προοδεύσει ακολουθώντας του παλιούς δρόμους,
ακόμα κι αν ο ρυθμός ήταν κατά διαστήματα κάπως αργός»[1]
Η οικονομική ανόρθωση της Αθήνας είναι αξιοσημείωτη
και νέα βιοτεχνικά κέντρα ανταγωνίζονται στην παραγωγή και στο εμπόριο, όπως τα
παράλια της Ιωνίας Μικράς Ασίας, οι Συρακούσες, ο Τάραντας κ.ά.
Η κεντρική ιδέα του ελληνισμού που είναι η ιδέα της
πόλης –
κράτος, εκείνη την εποχή βρίσκεται σε παρακμή. Όλοι οι παραδοσιακοί δεσμοί,
όπως για παράδειγμα θρησκευτικοί, κοινωνικοί και αστικοί κλονίστηκαν. Αντίθετα
προβάλλεται η ιδέα του ατόμου και γενικότερα του ανθρώπινου γένους
οι οποίες άλλοτε συγκρούονται και άλλοτε αναπτύσσουν σχέση συμπάθειας.
Ο Πλάτων υπήρξε ο μεγάλος δημιουργικός φιλόσοφος της εποχής του 4ου
αιώνα π.Χ., γεννήθηκε στην Αθήνα το 427 π.Χ. από γονείς της υψηλής
αριστοκρατίας.
Το έργο του Πλάτωνα είναι διαχρονικό και ποικίλο. Πρώτα απ’ όλα
υπήρξε εκτός από φιλόσοφος και σπουδαίος μαθηματικός στοχαστής. Ασχολήθηκε με
πολλά θέματα των μαθηματικών της εποχής του, δέχθηκε Πυθαγόρειες επιδράσεις από
τον Αρχύτα τον Ταραντίνο και έθεσε βαθύτατα το ίχνος της σκέψης του στην
εξέλιξη των μαθηματικών. Εξάλλου σημαντική ήταν και η προσφορά της Ακαδημείας
του, γιατί εκεί δίδαξαν σπουδαίοι μαθηματικοί της εποχής του.
Κατά την περίοδο αυτή του 4ου π. Χ. αιώνα, γίνεται προσπάθεια να
εξελιχθεί η μαθηματική επιστήμη ως προς το σκοπό της, αλλά και ως προς τη μέθοδο. Κυρίαρχες μορφές αυτήν την περίοδο εκτός του
Πλάτωνα είναι
πλειάδα μαθηματικών, όπως ο Θεαίτητος, ο Εύδοξος, ο Αρχύτας, ο
Αριστοτέλης, ο Μέναιχμος, ο Φίλιππος ο Οπούντιος, ο Λεωδάμας ο Θάσιος, ο Λέων ο
Βυζάντιος κ.ά.
2. Η τριλογία:
Τίμαιος- Κριτίας- Ερμοκράτης
Ο διάλογος που φέρει το όνομα
«Τίμαιος», είναι ένα από τα πλέον σημαντικά
έργα του Πλάτωνα, όπου αναπτύσσονται οι απόψεις του μεγάλου αυτού φιλοσόφου
σχετικά με τη φυσική. Για το λόγο αυτό φέρει και τον υπότιτλο «Περί
φύσεως». Είναι ένα έργο που ανήκει στην τελευταία συγγραφική περίοδο του
Πλάτωνα και έχει περιεχόμενο κοσμολογικής φύσης καθώς και ανθρωπολογική
διάσταση.
Τα πρόσωπα που διαλέγονται στο έργο αυτό είναι ο Τίμαιος, ο Κριτίας, ο
Ερμοκράτης και ο Σωκράτης.
Ο διάλογος αυτός του Πλάτωνα φαίνεται να διαδραματίζεται στην εποχή
της Νικίειας ειρήνης (421 π.Χ.) ή λίγο νωρίτερα και έχει γραφεί περί το 360-347
π.Χ. [2]
Δύο βασικά στοιχεία ξεχωρίζουν στο διάλογο αυτό.
Το πρώτο είναι ότι κάθε τι που βλέπουμε και ακούμε ή μάλλον
γενικότερα κάθε τι που μπορούμε να το αντιληφθούμε με τις αισθήσεις ανήκει στον
λεγόμενο κόσμο του αισθητού και για το λόγο αυτό στον κόσμο της γενέσεως.
Άρα κάθε αισθητό αντικείμενο είναι αποτέλεσμα της δημιουργίας.
Το δεύτερο στοιχείο είναι η αιτιολόγηση αυτής της
δημιουργίας του αισθητού κόσμου είναι δηλαδή η απάντηση στο «γιατί». Η
αιτία της ύπαρξης των πραγμάτων που μας περιβάλλουν είναι ο δημιουργός. Είναι ο
μεγάλος τεχνίτης που κατασκεύασε τον κόσμο αυτό. Η δημιουργία του αισθητού
κόσμου έχει ως αρχικό υπόδειγμα κάτι το οποίο συγκεντρώνει όλα εκείνα τα
στοιχεία της τελειότητας, της αρμονίας και της ωραιότητας, τον κόσμο των ιδεών,
ο οποίος είναι αιώνιος και αμετάβλητος.
-
Η έννοια του Σύμπαντος
-
Το σύμπαν είναι ορατό και απτό. Υπ’ αυτήν την έννοια ανήκει
στον αισθητό κόσμο και συνεπώς είναι δημιούργημα του άριστου δημιουργού. Τα
στοιχεία, που προσδίδουν στο σύμπαν τις ιδιότητες να το βλέπουμε και να το
ακουμπάμε, είναι η φωτιά και η γη. Η φωτιά και η γη ως
τρισδιάστατες οντότητες συνδέονται μεταξύ τους με άλλα δύο «συνδετικά» στοιχεία.
Τον αέρα και το νερό. Έτσι τα τέσσερα αυτά στοιχεία συνθέτουν τον
κόσμο και το ευρύτερο σύμπαν με κάποια αναλογία και σταθερότητα. Η ιδέα αυτή
βέβαια προϋπήρχε και στους Ίωνες φιλοσόφους( Θαλή, Αναξίμανδρο, Ηράκλειτο κλπ)
καθώς και στον Ελεάτη φιλόσοφο τον Εμπεδοκλή ο οποίος έλεγε:
«Τέσσερα γαρ πάντων ριζώματα πρώτον άκουε»[3]
-
Τα δύο θεμελιώδη τρίγωνα
Ως βασικά και θεμελιώδη στοιχεία της δομής του κόσμου ο Πλάτωνας
θεωρεί δύο ορθογώνια τρίγωνα. Το ορθογώνιο και ισοσκελές τρίγωνο
καθώς και το ορθογώνιο τρίγωνο με μία οξεία γωνία ίση με 300. (Σχήμα 1)
τρίγωνο
καθώς και το ορθογώνιο τρίγωνο με μία οξεία γωνία ίση με 300. (Σχήμα 1)
Το πρώτο τρίγωνο οι πυθαγόρειοι το ονόμαζαν «μισό
τετράγωνο» γιατί προκύπτει από ένα τετράγωνο και το δεύτερο τρίγωνο
το «μισό τρίγωνο» γιατί προκύπτει από ένα ισόπλευρο τρίγωνο.
Τα τρίγωνα αυτά θεωρήθηκαν ως οι δομικοί λίθοι όλου του κόσμου γιατί
η ομορφιά τους ανάγεται στην απλότητα με την οποία συνδέονται οι γωνίες τους.
Δηλαδή:
Οι γωνίες του
πρώτου ικανοποιούν την σχέση:
, αφού
και
ενώ του δευτέρου τη σχέση:
γιατί
.
5. Τα τέσσερα
στερεά του Πλάτωνα
Κατά την αφήγησή του ο Τίμαιος αναφέρει ότι τα δύο ορθογώνια
τρίγωνα, το ορθογώνιο ισοσκελές και το ορθογώνιο σκαληνό, αποτελούν τα
πρωταρχικά και θεμελιώδη στοιχεία από τα οποία συντίθενται τα τέσσερα θεμελιώδη
στοιχεία της φύσης, δηλαδή το κανονικό τετράεδρο που παριστά τη
φωτιά, το κανονικό οκτάεδρο που παριστά τον αέρα(Σχ.2),
τον κύβο που παριστά τη γη και το κανονικό
εικοσάεδρο
που παριστά το νερό(Σχ.3).

Η επιλογή των δύο αυτών
τριγώνων δεν γίνεται τυχαία από τον Πλάτωνα για την κοσμογονία του, αλλά ύστερα
από μια έντονη αφομοίωση της πυθαγόρειας αντίληψης, η οποία θεωρούσε τους
αριθμούς ως το ουσιαστικότερο στοιχείο του κόσμου.

Ο Πλάτωνας διαφοροποιείται από τους υλιστές
Λεύκιππο και το
Δημόκριτο και διατυπώνει μια φιλοσοφία μαθηματικού τύπου.
«Οι ατομικοί θεωρούν ότι τα άτομα υπάρχουν αιώνια, ανεξάρτητα από
οποιαδήποτε υπέρτατη επέμβαση. Τα σχήματά τους έχουν οποιαδήποτε μορφή και είναι
το πλήθος και τα μεγέθη τους άπειρα. Ο Πλάτων όμως είναι εκείνος που θα διακόψει
τον πολυμορφισμό των ατομικών. Τα «άτομα» του Πλάτωνος δεν είναι υλικά σώματα,
αλλά επίπεδα γεωμετρικά σχήματα τα οποία ανήκουν στο νοητό κόσμο των Μαθηματικών
και είναι πεπερασμένα. Θεωρούμενα δε ως καθαρά μαθηματικά αντικείμενα έχουν
απελευθερωθεί από την έννοια της ύλης, ενώ μπορούν να μετασχηματίζονται το
ένα στο άλλο, ανταλλάσσοντας μερικά από τα τρίγωνά τους, χωρίς να
δημιουργείται κανένα κενό».[4]
6. Ο μετασχηματισμός της φωτιάς- η πρώτη εξίσωση
Γενικά, κατά την άποψη αυτή του Πλάτωνα, τα τέσσερα στερεά, που αποτελούν τα
τέσσερα στοιχεία της φύσης, θεωρούνται ότι είναι πολύ μικρά, ώστε οι επιμέρους
μονάδες από τις οποίες αποτελούνται, δηλαδή τα τρίγωνα, μένουν αόρατες. Το
ανθρώπινο μάτι βλέπει μόνο το αποτέλεσμα της συνάθροισης των πολλών επιμέρους
μονάδων.
«
Πρέπει ακόμα να αντιληφθούμε ότι ο Θεός, εφόσον η Ανάγκη πειθόταν να
υποχωρήσει με τη θέλησή της, καθόριζε επακριβώς τις αναλογίες που διέπουν το
πλήθος, τις κινήσεις και τις άλλες δυνάμεις των στοιχείων, και έτσι προχωρούσε
στην αρμονική συναρμογή τους» ( Τίμαιος 56c)
Με τη λογική αυτή ο Τίμαιος περιγράφει τον μετασχηματισμό του αέρα σε φωτιά και
αντίστροφα με την παρακάτω εξίσωση:
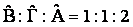
Η
σχέση αυτή δηλώνει ότι όταν «συναντηθούν» δύο ίσα μέρη από φωτιές, τότε η
«αρμονική τους συναρμογή» θα δώσει ένα μέρος από αέρα. Αυτό γίνεται γιατί αφού η
φωτιά αποτελείται από μικρά κανονικά τετράεδρα που σχηματίζονται από 24ορθογώνια
σκαληνά τρίγωνα, άρα τα δύο ίσα μέρη φωτιάς, θα περιέχουν πακέτα από 2Χ24=48
ορθογώνια τρίγωνα, τα οποία θα σχηματίσουν πακέτα των 48 τέτοιων τριγώνων,
δηλαδή πακέτα από κανονικά στερεά οκτάεδρα. Άρα δύο μέρη φωτιάς δίνουν ένα μέρος
αέρα.
7. Μετασχηματισμός της γης
Κατά την διαδικασία των μετασχηματισμών των τεσσάρων
στοιχείων, η γη είναι το μοναδικό στοιχείο το οποίο αποσυντίθεται στα επιμέρους
στοιχεία της, τα οποία είναι 48 ορθογώνια και ισοσκελή τρίγωνα και στη συνέχεια
ανασυντίθεται πάλι απ΄ αυτά στην αρχική της μορφή. Αυτό γίνεται διότι τα τρία
υπόλοιπα στοιχεία, φωτιά(τετράεδρο), αέρας(οκτάεδρο), νερό(εικοσάεδρο),
αποτελούνται από ορθογώνια σκαληνά τρίγωνα.
Έτσι, σύμφωνα με την ιδέα αυτή, η γη δεν μετασχηματίζεται σε άλλα
στοιχεία, όμως βοηθά στην επεξεργασία της αλληλομεταβολής και του
μετασχηματισμού των υπολοίπων στοιχείων. Ειδικότερα γράφει για το θέμα αυτό ο
Πλάτων:
«Όταν η γη συναντά τη φωτιά, αποσυντίθεται από την οξύτητά της
και διαχέεται – είτε η αποσύνθεση συντελεστεί μέσα στην ίδια τη φωτιά είτε μέσα
σε κάποιον όγκο αέρα ή νερού - , μέχρις ότου τύχει να ξανασυναντηθούν τα μέρη
της, να συναρμολογηθούν εκ νέου και να δώσουν πάλι γη, γιατί είναι αδύνατον τα
μέρη της γης να μετασχηματιστούν σε μέρη άλλου είδους» (Τιμ.56d)
Μετασχηματισμός του νερού – η δεύτερη εξίσωση
Με την ίδια λογική της αποσύνθεσης του αέρα σε δύο φωτιές
μπορούμε να εννοήσουμε και την αποσύνθεση του νερού σε δύο μερίδια αέρα και ένα
μερίδιο φωτιάς. Άρα:

δηλαδή ένα μερίδιο φωτιάς και δύο μερίδια αέρα
δίνουν ένα μερίδιο νερού.
Η εξίσωση (1) «ερμηνεύεται» από τη λογική ότι ένα μερίδιο νερού
αποτελείται από κάποιο αριθμό κανονικών εικοσαέδρων ή απλούστερα μπορούμε να
θεωρήσουμε ότι αποτελείται από ένα κανονικό εικοσάεδρο, το οποίο ως γνωστό
συντίθεται από 120 ορθογώνια σκαληνά τρίγωνα. Τα 120 αυτά τρίγωνα αναλύονται σε
δύο ομάδες, η πρώτη με 24 τρίγωνα που θα αποτελέσουν ένα κανονικό τετράεδρο,
δηλαδή τη φωτιά και η δεύτερη ομάδα θα περιλαμβάνει 96 τρίγωνα τα οποία μπορούν
να σχηματίσουν δύο κανονικά οκτάεδρα από 48 τρίγωνα το καθένα, δηλαδή δύο
στοιχεία του αέρα.
8. Η διάσπαση του αέρα σε νερό – η τρίτη εξίσωση
Κατά το μετασχηματισμό των θεμελιωδών στοιχείων, ο Πλάτων
θεωρεί, ότι ο αέρας κάτω από κάποιες συνθήκες μπορεί να μετασχηματιστεί σε νερό.
Η διαδικασία αυτή περιγράφεται στον Τίμαιο ως ένα γεγονός «ήττας» του στοιχείου
του αέρα. Η επικράτηση του νερού κατά τη διαδικασία αυτή καθώς και η διάσπαση
του αέρα, γίνεται σύμφωνα πάλι με τη θεωρία των κανονικών πολυέδρων.
Το κανονικό οκτάεδρο που αντιπροσωπεύει τον αέρα, περιέχει οκτώ
έδρες, οι οποίες είναι ισόπλευρα τρίγωνα, καθένα από τα οποία «χτίζονται»
από έξη ορθογώνια σκαληνά τρίγωνα. Άρα συνολικά περιέχει 48 τέτοια τρίγωνα.
Επίσης το νερό αντιπροσωπεύεται από το κανονικό εικοσάεδρο το οποίο περιέχει με
την ίδια λογική 120 τρίγωνα. Άρα εύκολα μπορούμε να αποκωδικοποιήσουμε τα λόγια
του Τίμαιου με την παρακάτω εξίσωση:
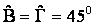
9. Ο μετασχηματισμός της φωτιάς σε νερό - η τέταρτη εξίσωση
Όταν τα σωματίδια της φωτιάς είναι λίγα απέναντι σε πολλά
και μεγαλύτερα σωματίδια άλλου είδους τότε το φαινόμενο οδηγείται στη διάσπαση
των σωματιδίων της φωτιάς και στο «σβήσιμο» με αποτέλεσμα να μετασχηματιστούν
και να γίνουν αέρας και από αέρας να καταλήξουν σε νερό. Αυτό συμβαίνει
σύμφωνα με την ανάλυση και τη σύνθεση των ορθογωνίων τριγώνων. Η σχέση –
αντίδραση με την οποία συντελείται τα γεγονός αυτό είναι η ακόλουθη:

Απόδειξη:
Από την (1) είναι:
και επειδή από την εξίσωση (3) είναι:
Άρα:
δηλαδή η σχέση (1)
Παρατηρούμε δηλαδή, ότι με τις σχέσεις αυτές, ο μεγάλος φιλόσοφος
της αρχαιότητας προσπαθεί να μοντελοποιήσει με θεμελιακούς νόμους, σύμφωνα με
τους οποίους συντελείται το γεγονός του μετασχηματισμού των στοιχείων της
φύσης. Τα στερεά του Πλάτωνα δίνουν σύμφωνα με το μοντέλο αυτό μια
ερμηνεία και σηματοδοτούν μια πορεία στην ιστορία των επιστημών και της
κοσμολογίας που ακόμα και σήμερα δεν έχει δοθεί πλήρης ερμηνεία.
10. Γενίκευση των μετασχηματισμών
Εφαρμόζοντας κανείς τη διοφαντική ανάλυση θα μπορούσε να
δημιουργήσει πλειάδα τέτοιων μετασχηματισμών και να διαπιστώσει τον τρόπο με τον
οποίο μπορούν να συντεθούν και να αναλυθούν τα τρία αυτά στοιχεία της πλατωνικής
κοσμολογίας.
Πράγματι ας αναζητήσουμε την αναλογία σύνθεσης της φωτιάς(Φ)
με τον αέρα(Α) ώστε να προκύψει το νερό(Ν). Αυτό ισοδυναμεί με την
αναζήτηση ακέραιων λύσεων της εξίσωσης:
όπου χ, ψ ακέραιοι που εκφράζουν τα μέρη της φωτιάς και του αέρα αντίστοιχα τα
οποία θα αναμιχθούν για να δώσουν ένα μέρος νερού και Φ, Α, Ν αριθμοί 24,48,120
που εκφράζουν τα ορθογώνια σκαληνά τρίγωνα του τετραέδρου, οκταέδρου και
εικοσαέδρου.
Λύση της (5)
Άρα η εξίσωση (5) γενικά γίνεται:
δίνοντας λοιπόν στο ψ διάφορες τιμές από το σύνολο των ακεραίων προκύπτει μια
σειρά άπειρων μετασχηματισμών που συνθέτουν τη φωτιά με το νερό για να δώσουν
ένα νερό. Δηλαδή:
(Εξίσωση
4)
(Εξίσωση
2)
κτλ.
Με τον ίδιο τρόπο θα μπορούσαμε να θεωρήσουμε τις εξισώσεις:
,
οι οποίες συνδέουν τη φωτιά με το νερό και δίνουν αέρα(εξίσωση 7), καθώς επίσης
τη φωτιά με τον αέρα και δίνουν νερό(εξίσωση 8).
Οι εξισώσεις αυτές είναι αντίστοιχα ισοδύναμες με τις:
,
Η εξίσωση (9) για
ψ=0 θα δώσει το μετασχηματισμό:
(εξίσωση
1)
και η (10) για
ψ=5 δώσει τον μετασχηματισμό:
(εξίσωση
3).
11. Το πέμπτο
στοιχείο
«Έμεινε ακόμα μια κατασκευή, η πέμπτη. Αυτή την κατασκευή ο Θεός την προέβαλε
στο σύμπαν, και το διακόσμησε περιχαράσσοντας το με αυτήν» (Τίμαιος 55c)
Η αινιγματική αυτή αναφορά του Πλάτωνα στον Τίμαιο συμπληρώνεται σε
ένα άλλο έργο του, το οποίο φέρει το όνομα «Επινομίς», όπου ξεκάθαρα ο
μεγάλος φιλόσοφος εισάγει το πέμπτο στοιχείο της κοσμογονίας του, τον «αιθέρα», του οποίου το στοιχειώδες σώμα είναι το κανονικό δωδεκάεδρο(Σχ.8).
«Υπάρχουν πέντε κανονικά γεωμετρικά
σώματα, και μπορούμε ν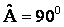 α
διακρίνουμε πέντε αντίστοιχες μορφές ύλης – γη, νερό, αέρα, φωτιά και αιθέρα –
καθώς και πέντε αντίστοιχα είδη ζώων, το καθένα με το κατάλληλο περιβάλλον
διαβίωσής του» (Νόμοι – Επινομίς: 981c-982a)
α
διακρίνουμε πέντε αντίστοιχες μορφές ύλης – γη, νερό, αέρα, φωτιά και αιθέρα –
καθώς και πέντε αντίστοιχα είδη ζώων, το καθένα με το κατάλληλο περιβάλλον
διαβίωσής του» (Νόμοι – Επινομίς: 981c-982a)
Ο αιθέρας κατά την άποψη αυτή αποτελεί την
«πέμπτη ουσία» από όπου προέρχεται και ο όρος «πεμπουσία»
και είναι το καθαρό γαλάζιο
ανώτερο στρώμα του αέρα. Κατ’ επέκταση ο αιθέρας συμβολίζει τον ουρανό, όπου
κατοικούσαν οι θεοί κατά την αντίληψη της εποχής εκείνης. Η λέξη αιθήρ παράγεται
από το ρήμα αίθω που σημαίνει: ανάπτω, καίω.(Μέγα Λεξικό της
Ελληνικής Γλώσσης, H.G.
Liddel – R.Scott).
12. Οι σύγχρονες
απόψεις
Η μελέτη των ιδιοτήτων των στερεών του Πλάτωνα(Solides de
Platon) κατά την πορεία της εξέλιξης των μαθηματικών κατέχει
πρωτεύουσα θέση και συνδέθηκε με μεγάλα ονόματα όπως του Πυθαγόρα, Θεαίτητου, Ευκλείδη, Αρχιμήδη, κι αργότερα του
R.Descartes
, του L. Euler[5],
J. Kepler,κ.ά. Επίσης
πολλοί ζωγράφοι εμπνεύστηκαν από την ομορφιά των στερεών αυτών όπως ο Α.
Durer, L. Pacioli,
L.Da Vinci κ.ά.
Τελευταία οι απόψεις του Πλάτωνα σχετικά με την κοσμολογία έρχονται
στην επικαιρότητα καθώς από την έρευνα μιας ομάδας πέντε Γάλλων και Αμερικανών
ερευνητών με επικεφαλής τον Jean –
Pierre Luminet του εργαστηρίου
LUTH (Laboratoire
Univers et Théories) που εδρεύει στο
Αστεροσκοπείο Meudon του Παρισιού, φαίνεται να
προκύπτει ότι το κανονικό δωδεκάεδρο εκφράζει τη μορφή του σύμπαντος. Σύμφωνα
με τη μελέτη των αστροφυσικών αυτών, το σύμπαν θεωρείται ότι είναι ένα «πεπερασμένο δωδεκαεδρικό σύμπαν»
το οποίο έχει το σχήμα μιας μπάλας
ποδοσφαίρου! (Σχ. 9). (Περιοδικό «Nature»
9/10/2003). [6],[7],[8].
(Laboratoire
Univers et Théories) που εδρεύει στο
Αστεροσκοπείο Meudon του Παρισιού, φαίνεται να
προκύπτει ότι το κανονικό δωδεκάεδρο εκφράζει τη μορφή του σύμπαντος. Σύμφωνα
με τη μελέτη των αστροφυσικών αυτών, το σύμπαν θεωρείται ότι είναι ένα «πεπερασμένο δωδεκαεδρικό σύμπαν»
το οποίο έχει το σχήμα μιας μπάλας
ποδοσφαίρου! (Σχ. 9). (Περιοδικό «Nature»
9/10/2003). [6],[7],[8].
Το θέμα βέβαια δεν είναι απλό και τα μαθηματικά που
υποστηρίζουν την άποψη αυτή είναι προχωρημένα και δύσκολα. Σχετικά με το
κανονικό δωδεκάεδρο και το προτεινόμενο μοντέλο της ομάδας του
Jean – Pierre Luminet,
συνδέεται άμεσα και το όνομα ενός μεγάλου Γάλλου Μαθηματικού του
Jules Henri Poincaré(1854 – 1912) ο οποίος
μελέτησε πολλές ιδιότητες του όμορφου αυτού στερεού.[9]
Με το δωδεκάεδρο συνδέεται τέλος, η
θεωρία των γραφημάτων(W.
Hamilton,1859)[10],
η θεωρία των
«ομάδων περιστροφής» (groupes de rotation)[11]
της Άλγεβρας, η οποία μελετά τις ιδιότητες των στερεών αυτών καθώς
περιστρέφονται γύρω από διάφορους άξονες, καθώς επίσης και η «Αλγεβρική
Τοπολογία»(Poincaré)[12], η οποία
μελετά τοπολογικές ιδιότητες και των στερεών αυτών.
Résumé
Platon, philosophe grecque
du 4ème siècle avant .J.C. c` est lui qui croyait à l` existence du
monde des idées et estimait que les hommes sont captives par le monde visible. À
Timée analyse ses opinions qui concernent la création du monde et introduit un
modèle qui se base sur les mathématiques et surtout sur les quatre solides
régulières : le tétraèdre, l` octaèdre, l` icosaèdre et le cube. Platon
considère que les plus petites pièces qui forment les quatre solides sont deux
triangles orthogonaux. Le triangle orthogonal et isocèle et le triangle
orthogonale et scalène qui sont le demi d` un carrée l`un et d` un triangle
équilatéral l` autre. Ce modèle idéaliste de la cosmologie diffère de celui de
Démocrite et Leucippe, parce que Platon considère que l`étude et l` usage des
mathématiques et surtout de la géométrie c`est une condition fondamental
d`examiner le monde. Aujourd`huit ces pensées de Platon revient plus que
toujours dans l` actualité. Le dodécaèdre, le cinquième solide de Platon prétend
d` être le schéma d` univers.
Παραπομπές
[1]
BOSTFORD&ROBINSON.
Αρχαία Ελληνική Ιστορία.Γ΄Έκδοση. Μορφωτικό Ίδρυμα Εθνικής
Τραπέζης. Αθήνα 1985.(σελ.413)
[2]
Α.Ε.Taylor.
ΠΛΑΤΩΝ ο άνθρωπος και το έργο του. Μορφωτικό Ίδρυμα Εθνικής Τραπέζης.
Αθήνα 2003.(σελ.497)
[3]
Γιάννης
Τζαβάρας..Η ποίηση του Εμπεδοκλή. Εκδόσεις Δωδώνη.1988
[4]
Χ.Π. Φίλη. Η
Γεωμετρική θεώρηση της ύλης από τον Τίμαιο.(σελ.72-73). Φιλοσοφία.
Επετηρίς του Κέντρου Ερεύνης της Ελληνικής Φιλοσοφίας. Ανάτυπον. Αθήναι.
2002.
[5]
Δ.Α.Αναπολιτάνος. Εισαγωγή στη Φιλοσοφία των Μαθηματικών. Εκδόσεις
Νεφέλη. Αθήνα 1983 (σελ.46)
[6]
Εφημερίδα:
Le monde.
De nouvelles measures
relancent le debat sur la forme de l’ univers.18 juin 2003
[7]
Εφημερίδα:
Libration. 10 Octobre
2003.
[8]
J.P.Luminet.
Conférence sur « La forme de l’espace » 10/6/2005
http://www.planetastronomy.com/special/2005-special/luminet-formuni-iap-10juin2005.htm.
[9]
Jon
Milnor.Vers la conjecture de Poincare et la classification des variétés
de dimension 3. SMF-Gazetta-99.Janvier 2004.
[10]
Χρόνης
Μωυσιάδης. Συνδυαστική Απαρίθμηση. Εκδόσεις Ζήτη.
[11]
J.M.Lemaire.
Les mathématiques au CNRS, évolutions et nouvelles réalités. (« math.en.jeans »
en 1996)
http://mathenjeans.free.fr/anej/édition/actespdf/96085099.pdf
[12]
C.
Camalon. Les solides de Platon. AbraCAdaBRI No 5 Sept-Oct.
1994
Βιβλιογραφία
1.
Πλάτων. Τίμαιος(ή περί φύσεως). Εκδόσεις Κάκτος
2.
Πλάτων. Νόμο ι- Επινομίς. Εκδόσεις Κάκτος.
3.
H.G.
Liddel–R.Scott.
Μέγα Λεξ. της Ελ. Γλώσσης. Εκδ
:Ι.
Σιδέρης.
Αθήνα
4.
E.Chaney. La face cachée des polyèdres. http://irem.u-strasbg.fr
5.
Περιοδικό: Nature.
9 Οκτωβρίου 2003



 τρίγωνο
καθώς και το ορθογώνιο τρίγωνο με μία οξεία γωνία ίση με 300. (Σχήμα 1)
τρίγωνο
καθώς και το ορθογώνιο τρίγωνο με μία οξεία γωνία ίση με 300. (Σχήμα 1)

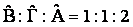

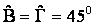

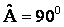
 (
(